This meets the requirements. Unpacking the meaning from that complex definition can be difficult.
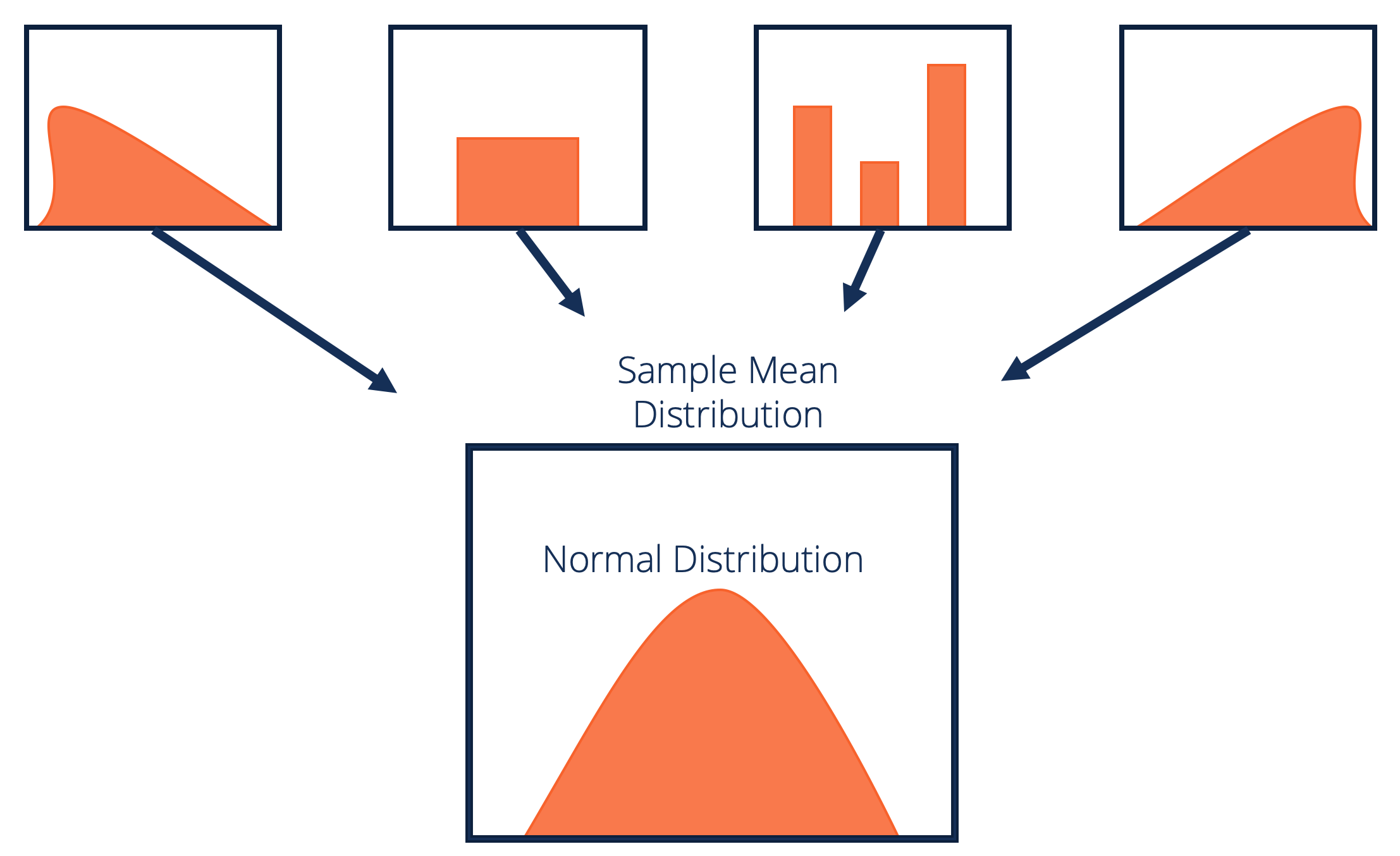
Central Limit Theorem Overview History And Example
For example college students in US is a population that includes all of the college students in US.
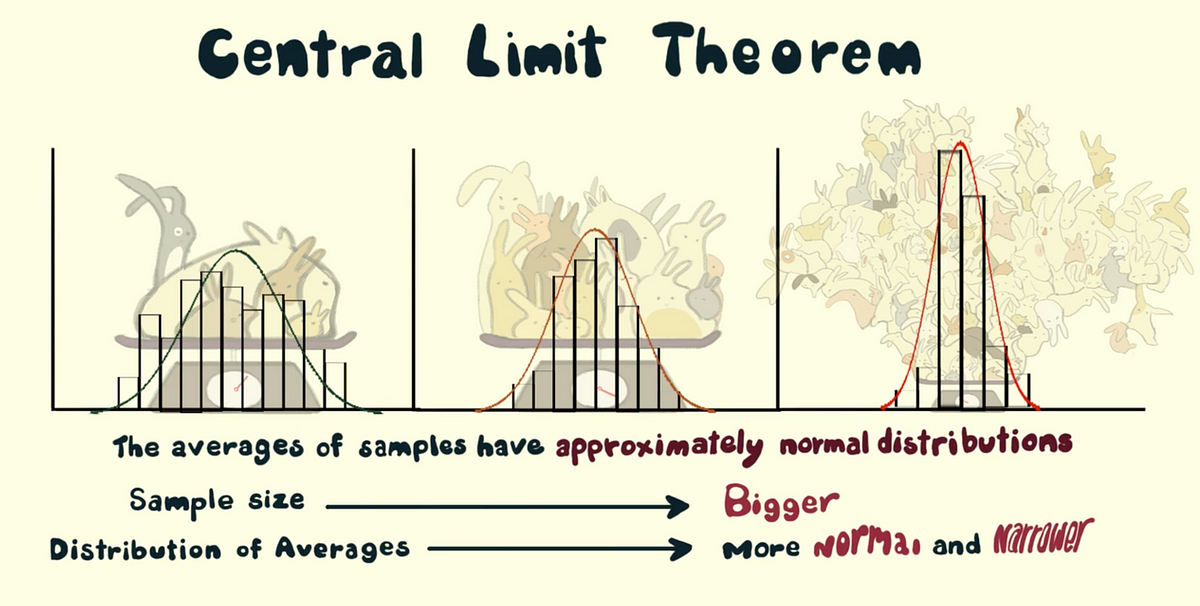
. Basic Statistics 9th Edition Edit edition Solutions for Chapter 7 Problem 10P. Any of several fundamental theorems of probability and statistics that state the conditions under which the distribution of a sum of independent random variables is approximated by the normal distribution especially. This fact holds especially true for sample sizes over 30.
In your own words explain the central limit theorem. The central limit theorem explains why the normal distribution arises so commonly and why it is. The central limit theorem CLT is a fundamental and widely used theorem in the field of statistics.
What is the central limit theorem Please describe it in your own words. The Central Limit Theorem which is widely regarded as the crown jewel of probability and. Describe an experiment that could be used to verify the central limit theorem.
Thus if the theorem holds true the mean of the thirty averages should be. The Central Limit Theorm. The central limit theorem tells us exactly what the shape of the distribution of means will be when we draw repeated samples from a given population.
Describe the Central Limit Theorem in your own words. The central limit theorem also tells us that no matter what the distribution of the population is the shape of the sampling. The Central Limit Theorem in probability theory a theorem that establishes the normal distribution as the distribution to which the mean average of almost any set of independent and randomly generated variables rapidly converges.
Q9bi Explain the reason for the statisticians statement. Thus P 2 7 C 2 064 2 1-064 7-2 00520. The central limit theorem allows us to use a normal distribution for some very meaningful and important applications.
The mean of the sampling distribution will be equal to the mean of the. Before selling it a researcher wants to test its effectiveness. The central limit theorem in statistics states that given a sufficiently large sample size the sampling distribution of the mean for a variable will approximate a normal distribution regardless of that variables distribution in the population.
This means we can use the binomial probability formula. Fixed number of trials trials are independent two possible outcomes use or do not use and the same probability of success use for all trials. This approximation improves as we increase the size of the simple random samples.
The population mean for a six-sided die is 1234566 35 and the population standard deviation is 1708. B No - route B journey times are normally distributed. Indicate where if anywhere in this question you needed to make use of the Central Limit Theorem.
Further as discussed above the expected value of the mean μ x μ x is equal to the mean of the population of the original data which is what we are interested in estimating. The taxi journey times are not known to be normally distributed. The Central Limit Theorem provides more than the proof that the sampling distribution of means is normally distributed.
For those new to statistics this definition may seem a bit intimidating. D Yes - Car journey times are from an unknown distribution. The central limit theorem states that the sampling distribution of the mean approaches a normal distribution as the sample size increases.
Specifically as the sample sizes get larger the distribution of means calculated from repeated. This brief tutorial explains what the central theorem tells us and why the result is important for statistical inference. The central limit theorem states that the sampling distribution of a sample mean is approximately normal if the sample size is large enough even if the population distribution is not normal.
A No - route A journey times are normally distributed. Definition of central limit theorem. The central limit theorem states that for a large enough n X-bar can be approximated by a normal distribution with mean µ and standard deviation σ n.
State why use of the Central Limit Theorem was required in calculating this confidence interval. In other words the central limit theorem states that for any population with mean and standard deviation the distribution of. The central limit theorem says that this sampling distribution is approximately normalcommonly known as a bell curve.
The central limit theorem also states that the sampling distribution will have the following properties. If you go three standard deviations below the mean youre at -. Central limit theorem is a statistical theory which states that when the large sample size has a finite variance the samples will be normally distributed and the mean of samples will be approximately equal to the mean of the whole population.
The central limit theorem CLT states that the means of random samples drawn from any distribution with mean m and variance s2 will have an approximately normal distribution with a mean equal to m and a variance equal to s2 n. According to the Central Limit Theorem the arithmetic mean of a sufficiently large number of iterates of independent random variables at. Therefore as a sample size increases the sample mean and standard deviation will be closer in value to the population mean μ and standard deviation σ.
Population is all elements in a group. The Central Limit Theorem CLT for short basically says that for non-normal data the distribution of the sample means has an approximate normal distribution no matter what the distribution of the original data looks like as long as the sample size is large enough usually at least 30 and all samples have the same size. The central limit theorem concerns the sampling distribution of the sample means.
We may ask about the overall shape of the sampling distribution. An educational enrichment company wants to sell an at home learning module for children that is intended to improve their scholastic ability. Before we go in detail on CLT lets define some terms that will make it easier to comprehend the idea behind CLT.
One which is much applied in sampling and which states that the distribution of a mean of a sample from a population with. Solutions for problems in chapter 7 1P. What you can do is collect many samples from weekly sales in your stores the population calculate their mean the average number of seltzer cases sold and build the.
It also provides us with the mean and standard deviation of this distribution. Why is it so important to statistics. The Central Limit Theorem tells you that we dont have to visit every single store in the region and get their seltzer sales numbers for the week to know how many cases to put in the next order.
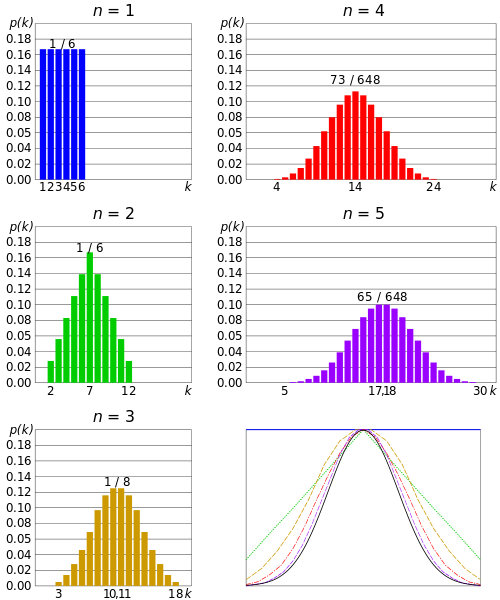
Central Limit Theorem Definition And Examples Statistics How To

Central Limit Theorem In Action And Examples From Its Practical By Ceren Iyim Towards Data Science

0 Comments